Vibrations and Waves

8 The Dispersion of Waves

8.1 THE SUPERPOSITION OF WAVES IN NON-DISPERSIVE MEDIA

8.1.1 Beats

The sum (blue) of two sine waves (red, green) is shown as one of the waves increases in frequency. The two waves are initially identical, then the frequency of the green wave is gradually increased by 25%. Constructive and destructive interference can be seen.

8.1.2 Amplitude modulation of a radio wave

An audio signal (top) may be carried by a carrier signal using AM or FM methods.

Illustration of amplitude modulation

Modulation depth. In the diagram, the unmodulated carrier has an amplitude of 1.

The power of an AM radio signal plotted against frequency. fc is the carrier frequency, fm is the maximum modulation frequency

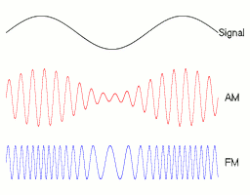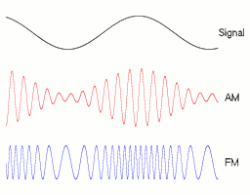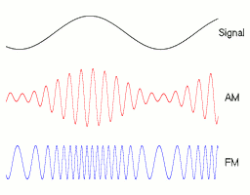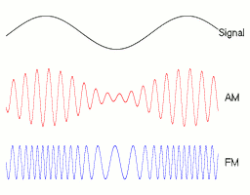
8.2 THE DISPERSION OF WAVES

Diagram illustrating the relationship between the wavenumber and the other properties of harmonic waves.

frequency $\omega$ is a function of the wavenumber $k$ :$\omega=\omega(k)$

8.2.1 Phase and group velocities

Frequency dispersion of surface gravity waves on deep water. The $\color{red}{ ▪︎ red\ dot}$ moves with the phase velocity, and the $\color{green}{ • green\ dots}$ propagate with the group velocity. In this deep-water case, the phase velocity is twice the group velocity. The $\color{red}{ ▪︎ red\ dot}$ traverses the figure in the time it takes the green dot to traverse half.

Two-frequency beats of a non-dispersive transverse wave. Since the wave is non-dispersive, $\color{red}{ •\ phase}$ and $\color{green}{ •\ group}$ velocities are equal.

• normal dispersion
• anomalous dispersion
• no dispersion

8.3 THE DISPERSION RELATION

• Dispersion of electromagnetic waves occurs in the propagation of radio waves in the ionosphere

  $$\omega^2=\omega_0^2+c^2k^2$$ $\omega_0$:plasma oscillation frequency

• For waves on deep water, where the wavelength is small compared with the depth of the water, the angular frequency ω and wavenumber k are related by the dispersion relation

  $$\omega^2=gk+\frac{Sk^3}{\rho}$$

8.4 WAVE PACKETS

8.4.1 Formation of a wave packet

bandwidth theorem

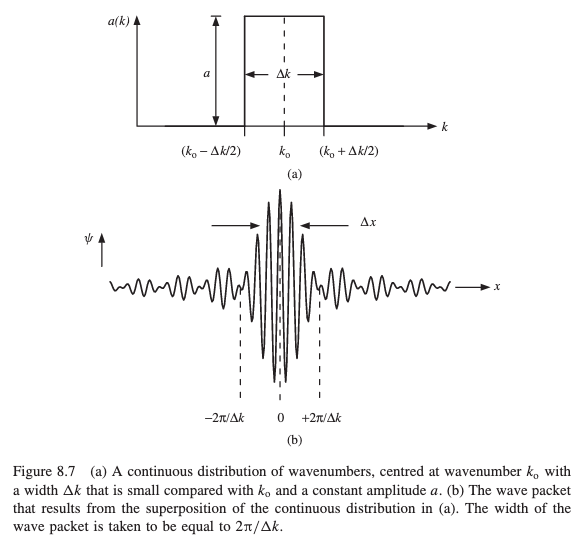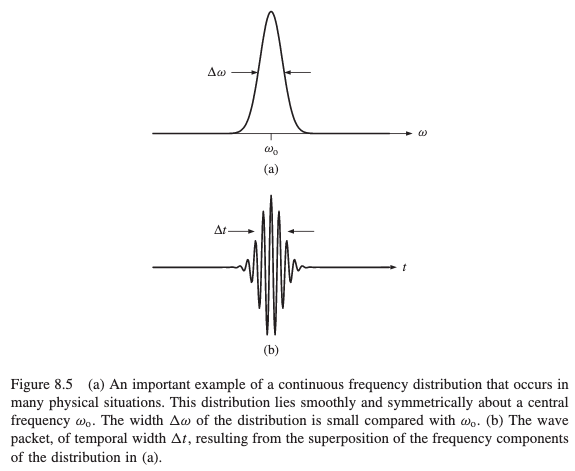$$\Delta x \Delta k \approx 2 \pi$$ $$\Delta t \Delta \omega \approx 2 \pi$$ Heisenberg Uncertainty Principle